日次景気DIの欠測補完と不確実性評価－状態空間モデルを軸とした実務設計

情報統括部　情報統括課
主席研究員　窪田剛士

帝国データバンク（以下, TDB）が毎月実施している「TDB景気動向調査」では、月次の景況感を表す指標として景気DIを公表してきた。同時に、日次単位の情報も保有し、その変化を捉えている。ただし、同調査は毎月後半に実施しており、月前半の日次データは欠測値となっている。そこで、状態空間モデルにより日次データを補完推計し、さらに日次の予測するモデルを開発した。本レポートでは、その基本的な考え方と方法、実務における活用例をまとめた。

【要約】

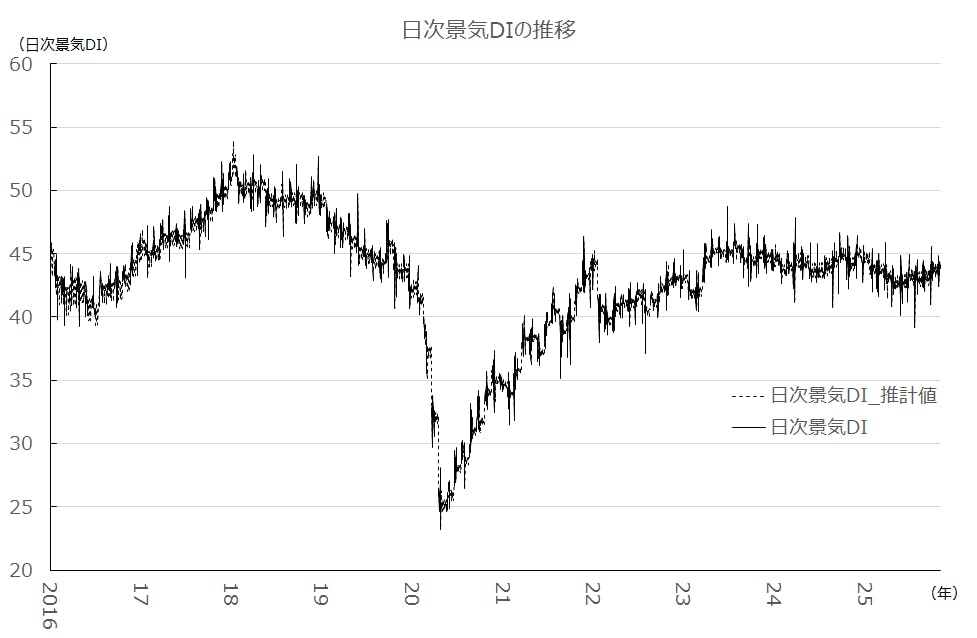
• TDB景気動向調査から得られる日次景気DIの欠測値を状態空間モデルで補完し、2014～2025年の連続系列と95％予測区間を構築した。
• 祝祭日、log(回答数)、株価・為替の対数リターンを外生変数とし、週内季節やトレンドを含むUCM（状態空間）とロバスト回帰を比較検証した。
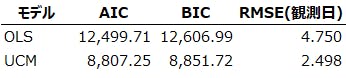
• AIC（赤池情報量規準）とRMSE（二乗平均平方根誤差）、残差診断で最適な仕様を選定し、UCMを最終モデルとすることで構造の時変性と欠測処理の一貫性・安定性を確保した。
• 在庫・人員配置・販促タイミングなどに予測区間を組み込み、実務的な意思決定ルールの活用例を提示した。

1. 目的と到達点

本レポートの目的は、2014年4月17日から2025年10月31日までの連続日次データについて、調査実施日以外に生じる欠測を自然なロジックで補完し、意思決定に使える一本化系列（点推計＋95％予測区間）を整備することにある。外生として祝祭日と回答数、さらに市場の短期情報を反映するために株価と為替レートを用いている。モデル比較は一貫してAICを主指標、観測日におけるRMSEを副指標とし、UCM（状態空間）とロバスト回帰（決定論的回帰）の優劣を検証したうえで、最終的にUCMを採用した。

意思決定の現場では、点推計の上下に広がる不確実性の幅が重要になる。したがって本稿は、単に数値を補う作業にとどめず、予測区間の幅が広がる日を早期に識別し、在庫や人員配置・販促タイミングなどの配分強度を調整するような、実務におけるルール設計にも活用可能とすることを狙いとしている。

2. データの構造と前処理

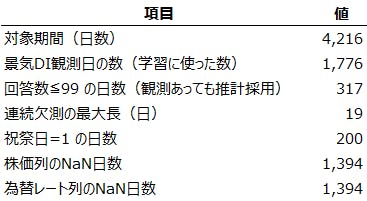
原データは、年月日と景気DIに加え、祝祭日や回答数、株価、為替レートが入る（表1）。厳密な日付を構成したうえで、対象期間のすべての日にちを連続に並べる。観測のない日は NaNのまま保持し、モデル内部で欠測処理を行う。外生変数の整形方針は次の通りとする。

• 祝祭日：0/1ダミー（欠損は0で整列）
• 回答数：スケール安定化のため log(1+回答数)
• 株価および為替：レベルではなく対数リターン（以下、Δlog）を使用

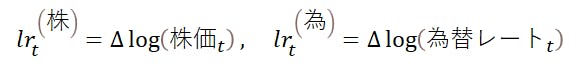
こうすることによりトレンドの混入を抑え、短期ショックの寄与を安定に捉えやすくなる。

【表１　入力データの項目と構造】

また、回答数が小さすぎる日（閾値〈しきいち〉以下。任意に設定）は観測値の信頼性が落ちやすいので、学習時はNaNとして扱い、実運用では推計した結果を採用する。これは「データ品質が推計品質を左右する」という前提に沿った実務的な選択である。

3. 方法論の骨格

3.1 状態空間（UCM）の観測方程式と状態方程式

UCMは観測と潜在構成要素を分ける。観測方程式は

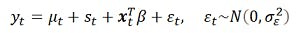
で与える。ここで yt は日次の景気DI、μt は潜在レベル、st は週内季節（周期7）、xt は外生ベクトルである。本件では

を採用する。状態方程式は潜在レベルをランダムウォークで表し、

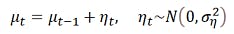
週内季節 st は和ゼロ制約を満たす確率的成分として実装する。この枠組みにより、欠測が混在してもカルマンフィルタ／平滑化で自然に扱うことが可能となる。観測日には観測値に情報が強く寄る一方、欠測日には前後の文脈と外生的な情報によって最も整合的な推計が与えられる。

3.2 ロバスト回帰の比較枠組み

比較のための決定論的モデルは、次のような回帰式で表す。

ここで f(t) は二次のトレンド項、年次Fourierは通常 K=3、曜日は月曜日を基準とした6本のダミー変数とする。ロバスト回帰は、係数の解釈は直観的で計算も軽いことがメリットになるが、構造が時期によって変化する特性や端点不確実性の扱いではUCMに劣る。

4. 推定、比較、選定

推定では、まず学習に用いる目的変数として、回答数が閾値以下の日とそもそも景気DIが欠測の日をNaNとした系列を用意し、UCMに投入する（モデル構造は表2を参照）。欠測はカルマンフィルタ／平滑化の内部で自然に扱われ、パラメータは最尤法で推定する。同じデータ・同じ外生を用いてロバスト回帰も推定し、両者について対数尤度と有効パラメータ数からAICを算出し、評価する。AICは

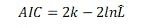
で定義され、値が小さいほど望ましい。

AICが十分に小さい方を第1候補とし、差が僅少な場合には観測日におけるRMSEを見て、過度の滑らかさや過適合になっていないかを確認する。さらに、端点の過適合や系列が持つ特性は、残差の自己相関や外生変数の係数の符号・大きさが直観と整合しているかを点検（Ljung–Box検定）する。UCM側はレベル／週内季節／AR(1)誤差の有無を入替え、回帰側はFourier次数K・曜日ダミー・トレンド次数の感度分析を行う。最終的にはAICが最小の仕様を採用しており、本分析ではUCMが最終モデルとして選択された（表3）。

【表２　UCM（状態空間）のモデル構造】

【表３　モデルの選定】

5. 推計値と不確実性の提示

すべての日次データについて、観測日は「景気DI_実績」を保持し、欠測日はUCMの平滑化推計で補完する。また、各日に95％予測区間を付す。正規近似に基づけば、時点 𝑡 の予測分散を Var(y^t ) とおき、

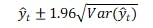
で区間が与えられる。ただし、端点近傍では前後情報の非対称性から分散が大きくなりやすく、帯が広がる傾向が生じるが、これは異常ではなく、不確実性の自然な反映である。

6. 外生効果の解釈

外生変数の係数ベクトル 𝛽 は、それぞれの変数が景気DIに与える平均的なインパクトを示す（表4）。祝祭日の係数が負であれば、営業活動や回答行動の鈍化を通じて、同水準のトレンド・週内季節のもとでは景況感がやや弱く出る、という構造を意味する。これに対して log(1+回答数) の係数が正の場合、回答が厚いほど情報のばらつきが抑えられ、安定性のあるDIが観測される傾向があると解釈することができる。

株価リターンの係数は、市場の上げ下げがマインドにどの程度即時に波及するかを表し、有意に正なら「株高＝景況感の押し上げ」がデータ上確認されたことになる。為替リターンについては、輸出入など業種構成によって符号が分かれ得るため、推定結果を見ながら、自社の感覚と整合するかを慎重に吟味する必要がある。

【表４　UCMの係数表】

株価・為替の対数リターンは短期の市況ショックに対する景況感の敏感度を捉え、当日の変動を推計へ取り込む。回帰モデルの係数表は、UCMにおける外生効果の直観整合性を手元で素早く点検する補助線として役立つ。

また、これらの効果はトレンドや週内季節を控除したうえでの“増分”であり、単純相関ではなく、他の要因を制御した条件付きの感応度として解釈するのが適切である。

7 将来予測と外生シナリオ

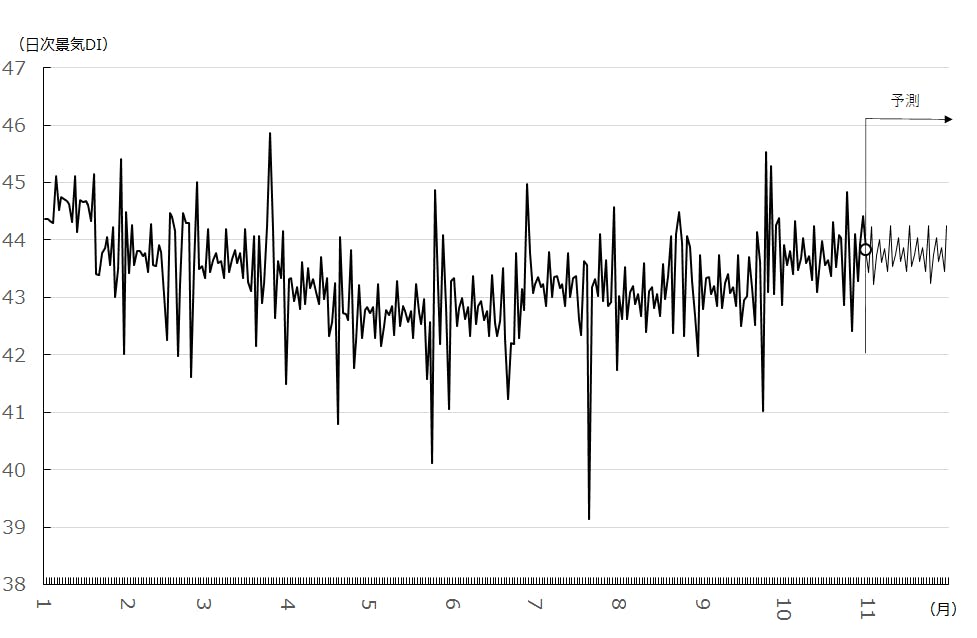
ここまでの議論は、主として「観測期間内」での欠測補完と不確実性評価に焦点を当ててきたが、実務で最も関心が集まるのは「これから先どうなりそうか」という将来予測である。状態空間モデル（UCM）は、インサンプルの平滑化だけでなく、外生変数のパス（シナリオ）を与えることで、多段先の予測を自然に生成することができる。とくに本レポートでは、祝祭日・回答数に加え、株価・為替レートの対数リターンを外生として組み込んでいるため、日々変動する市況環境を踏まえた短期予測が可能になる。今後30日間の予測結果が図1である。

【図１　2025年の日次景気DIの推移と30日間予測】

7.1 UCMにおける多段先予測の考え方

UCMの観測方程式を改めて書くと、

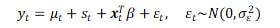
である。ここで μt と st はカルマン平滑化によって、最終観測時点 T までの情報を用いて推定される。この平滑化結果を初期条件として、将来 h ステップ先までの状態 (μT+1,sT+1),...,(μT+h,sT+h) を順々に予測し、対応する外生ベクトル xT+1,...,xT+h を与えれば、各将来時点の予測分布

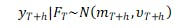
が得られる。この mT+h が点予測（期待値）、νT+h が予測分散に対応する。したがって、将来予測を実際に運用に落とし込む際には、

1. 直近までの観測に基づいて状態を平滑化する
2. 将来の外生パス（祝祭日・回答数・株価リターン・為替リターン）のシナリオを用意する
3. シナリオ別に mT+h と νT+h を計算し、予測区間を得る

という三段の流れを踏むことになる。このうち、1.はモデル推定と一体で自動的に行われるので、実務上の工夫の余地が大きいのは2.、すなわち外生パスのシナリオ設計である。

7.2 祝祭日と回答数のシナリオ

祝祭日は、カレンダー情報から機械的に生成できる。日本であれば jpholiday のようなライブラリを用いて、各将来日付が祝日かどうかを判定し、0/1のダミー系列として与えればよい。この部分にはモデルの主観が入りにくく、将来予測における“不確実性の源泉”になることは少ない。

回答数については、将来の値が直接はわからないため、実務的なルールが必要になる。今回の分析では、直近28日間の回答数分布から中央値を取り、

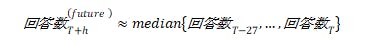
というシンプルな近似を採用している。この定数パスに対して log(1+・) を施し、将来の log(1+回答数) としてUCMに渡すかたちである。もちろん、実運用では「月初は回答が厚くなりやすい」「特定の曜日に偏る」といった知見を加味して、将来の回答数を曜日別平均で置き換える、あるいは別の補助モデルで予測した値を使うといった高度化も可能である。重要なのは、回答数が将来予測において「測定精度」の役割も担っている点であり、無造作に小さい値を与えると、モデル全体の不確実性を過小評価したり、逆に過大評価したりするリスクがある、ということである。

7.3 株価・為替レートのシナリオ設計

株価と為替レートについては、水準ではなく対数リターンを外生として用いている。これは、長期トレンドや水準の違いを直接モデルに持ち込まず、短期的な変動が景況感に与えるインパクトに焦点を当てるための設計である。将来予測では、これらリターンのパスをどのように想定するかが、予測の性質を決定づける。

基本的な考え方としては、次のようなシナリオを用意しておくと扱いやすい。

• ベースラインシナリオ：

  株価・為替ともにリターン0（横ばい）を想定する

  

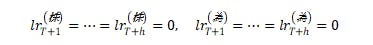
• 強気シナリオ：

  株価が一定のプラスリターン（例：+1％相当／日相当）、為替は円安方向に1％／日程度進む、といった仮定を置く

• 弱気シナリオ：
  株価が連日マイナスリターン、為替は円高方向に進む、といった想定でリターンをマイナスに固定する

今回の分析では、SCENARIO_LR_STOCK と SCENARIO_LR_FX を一定値として与え、将来の各日にその値を代入することで、上記のようなシナリオを表現している。もちろん、1日ごとに異なるパス（例：急落→横ばい→じわ戻し）をCSVなどから読み込み、よりリッチなシナリオパスを供給することもできる。ここで大事なのは、「将来の株価・為替がどうなるか」自体を見つけにいくのではなく、「もしこの程度の変動がしばらく続いたら景気DIはどの程度動き得るか」という感応度分析に重心を置くことである。

7.4 シナリオ別予測値の比較と運用

シナリオ別の予測値と予測区間を並べると、次のような問いに答えやすくなる。

• 市場が落ち着いている前提（横ばい）と、強気・弱気シナリオで、景気DIの上振れ・下振れの幅はどれくらい違うか
• ある日付 t に注目したとき、ベースラインではDI=50を上回らないが、強気シナリオでは区間上限が大きく上に抜け、弱気シナリオでは区間全体が下に沈む、といった形になっていないか
• 販促キャンペーンや大型投資の実行日を、どのシナリオでも「そこそこ安全な」位置に置けるかどうか

たとえば、直近30日先までのDIについて、横ばい・強気・弱気の3本の予測線と、それぞれの95％予測帯を重ねて描けば、「市場環境の変動に対する景気DIのレンジ」が視覚的に把握できる。このとき、ベースラインシナリオでは帯が閾値50の周辺を跨いでいるが、強気シナリオでは帯全体が上側に移動し、弱気シナリオでは逆に下側にずれる、といった構図が見えてくるはずである。こうした構図を前提に、リスク許容度に応じた意思決定（たとえば「どのシナリオでも下限が50を大きく割らない期間のみで販促を打つ」といったルール）を策定することができる。

7.5 予測区間の解釈とシナリオの組み合わせ

UCMでは、将来時点 T+h の予測分散 νT+h は、状態の不確実性と外生の効果を織り込んだ形で計算される。予測区間は

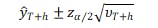
の形をとるので、シナリオパスを変えると、 y^T+h の位置（帯のセンター）が動き、必要に応じて分散自体も変化する。株価・為替リターンの振れ幅が大きいシナリオを想定すると、外生変数の影響で系列がより振られ、結果として変動幅が広がることもある。このため、「変動幅の広がり」を単なるノイズと見るのではなく、「そのシナリオの下でどれだけ振れ得るか」という意味で解釈する姿勢が重要になる。

また、「ベースライン＋ショック」のような構成も有効である。具体的には、横ばいシナリオを基準としながら、特定の日だけ大きな株価下落・為替急変を仮定し、その日の前後でDIの予測帯がどの程度歪むかを見ることで、「ショックの影響範囲と回復速度」を定性的に把握することができる。この種の分析は、危機対応計画やストレステストと相性がよい。

7.6 実務への落とし込み

実務に組み込む際は、すべてのシナリオを日次で細かく追う必要はない。むしろ、月次あるいは週次の定例会において、「次の1カ月について、ベースライン・強気・弱気の3シナリオでDIのレンジはこうなる」といった要約図を提示し、そのレンジの中で在庫計画・人員配置・販促スケジュールなどが妥当かをチェックする使い方が現実的である。

まとめると、将来予測と外生シナリオは、「未来を当てるための道具」というよりも、「さまざまな前提の下で、景気DIがどの程度まで振れ得るか」を見せるための可視化レイヤーとして活用するのが良い。UCMを核にした今回の設計は、そのための土台をすでに備えており、あとはシナリオの粒度と頻度を現場の意思決定サイクルに合わせて調整していけば、日次の景況感指標が、より戦略的な計画立案に直接つながっていくはずである。

8. 実務インプリケーション（在庫・人員・販促・意思決定）

ここでは、それぞれの業務を行う際、本レポートで構築した予測モデルやその結果を実務においてどのように活用することができるか、いくつかのケースを取り上げる。

8.1 在庫／発注

• 下限帯が需要想定を割る局面は追加発注を慎重化、上限帯が強ければ早めの積み増し。

在庫と発注の意思決定に使う場合、日次の景気DIそのものよりは、「想定需要に対する上振れ・下振れリスク」の指標として解釈するのが扱いやすい。たとえば、DI が50を「平常」レベルとみなすのであれば、予測区間の下限が50を大きく割り込む局面は、需要が弱めに出るリスクが顕在化している状態とみなせる。このときは安全在庫を維持しつつも、追加発注については慎重なスタンスをとり、納期に余裕のある案件の前倒し発注は抑制する判断が合理的になる。一方で、予測区間の上限が50を明確に上抜けており、かつ帯の幅がそれほど広くない場合には、需要が強い方向に振れる確率が高まっていると解釈できるため、早めの積み増しやリードタイムの短い仕入先へのシフトなど、攻めのオペレーションを選択しやすくなる。重要なのは、点推計だけではなく「帯全体が閾値のどちら側にあるか」「帯の幅がどの程度か」を織り込んで、在庫水準と発注タイミングを調整するルールを明文化しておくことである。

8.2 人員配置

• 週内パターンと帯の幅でピーク日に重点配置。連休前後は柔軟運用。

人員配置では、週内パターンと予測区間の幅を組み合わせて判断するのが実用的であろう。UCMには週内季節が含まれているため、曜日ごとのピーク・ボトムが推計に反映されている。この特徴を利用して、たとえば「水曜・金曜は需要が高く出る傾向」などが明示されるなら、その曜日のうち、予測区間の下限が平常レベルを上回る日には、あらかじめ人員を手厚く配置しておく。一方で、連休前後や特異日では予測区間が広がりやすく、不確実性が高くなる。そのときは固定的なシフトではなく、可変枠やパートタイム・シフト交換の余地を残した配置に切り替え、当日の実績を見ながら柔軟に追随できる体制を整える方が望ましい。したがって、帯が狭くピークが明瞭な日は「前倒しの重点配置」、帯が広く読みにくい日は「柔軟性を重視した配置」という二段階の運用ルールを持つと、余剰人件費と機会損失のバランスがとりやすくなる。

8.3 販促タイミング

• 帯が狭い＆推計が上向きの時期に広告投下を濃く、帯が広い局面はA/Bテストを重視。

販促については、景気DIの推計が上向きかどうかに加えて、予測区間の狭さを一つの「自信度指標」として扱うとよい。帯が狭く、かつ推計値が明確に平常水準を上回る時期は、需要の追い風が比較的読みやすい局面といえるので、広告投下量を増やしたり、割引率をやや強めにするなど、攻めのキャンペーンを集中させる候補期間となる。逆に、帯が広く上振れ・下振れの両方の可能性が大きい時期は、過度に大きな予算を一括で投じるよりも、A/Bテストやマルチアームバンディットのような実験的投下を通じて「学習を稼ぐ」期間と位置づけた方が合理的である。その意味で、予測区間は単なる不確実性の表示ではなく、「どの局面で一気に踏み込むか」「どの局面で慎重に検証を重ねるか」を切り分けるスイッチとして使える。

8.4 意思決定ルール例

• DI推計が50±帯を上抜け／下抜けで、販促／コスト配分の自動トリガー。

最後に、実際の運用で使える意思決定ルールの例を挙げておく。たとえば、ある日 t における推計値 y^t と95％予測区間 [Lt,Ut] に対し、「基準DI=50」と決めておく。もし Lt>50 であれば、「その日は景況感が高水準である可能性が95％近い」という意味になるので、自動的に販促枠を増やしたり、在庫補充のトリガーをONにする。一方、Ut<50 であれば需要減のリスクが高いとみなし、広告投下を抑制したり、コスト削減モードに切り替える。区間が 50を跨いでいる場合は「不確実」のフラグを立て、意思決定を自動ではなく担当者の裁量に委ねる、あるいは追加情報（他指標や高頻度データ）を確認したうえで判断するフローに回す、といったルール設計が考えられる。このような閾値×帯の組み合わせでトリガーを定義しておくと、モデルの結果が日々のオペレーションに自然に結びつきやすくなる。

9. 限界と今後の拡張

ここまで、本分析で構築したモデルを説明、その結果の活用方法などを示してきた。しかし、UCMは柔軟だが万能ではない。突発的な制度変更、災害、猛暑などのイベントは、外生が不足していれば残差に表れる。これに対しては、イベントダミーの導入や、天候・カード消費・観光指標・価格系DI・営業日数などの外生的な要素を拡充することで一段と有効に働く可能性が高い。短期予測の厳密比較はローリング・アウトオブサンプルの誤差系列を用いたDiebold–Mariano検定で評価できよう。さらに、分位点回帰や状態空間のスケール混合を取り入れれば、上振れ・下振れリスクの非対称性も表現しやすくなる。

結語

本分析で構築した設計では、日次の景気DIに内在する欠測の常態と日々の不確実性とを、状態空間の枠組みで一貫性をもって扱う。また市場関連の短期情報を株価・為替の対数リターンとして取り込み、観測の薄い局面でも過度な外挿に走らず、確率的に変動幅と確度を可視化してきた。モデル比較ではUCMがAICで優位を保ち、RMSEも実務に堪える水準を示した。最終的に、一本化したデータ系列は点推計＋95％区間として運用へ直結する形になり、さまざまな資源配分の強弱や検証設計の巧拙に具体的な手掛かりを与えることが可能となっている。今後は外生的要素の拡充とシナリオ運用の高度化、ローリング評価の自動化を進めれば、組織内の「当たり前の意思決定インフラ」として、さらに信頼度が高まるはずである。